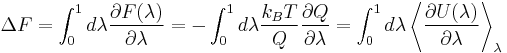Thermodynamic integration
Thermodynamic integration is a method used to compare the difference in the thermodynamic quantity of two given states (e.g., A and B) in molecular dynamics simulation. Free energy difference is one quantity commonly computed in this way; since they are not simply functions of the phase space coordinates of the system, but are related to the canonical partition function Q(N,V,T), they cannot be directly measured in a simulation. These differences are usually calculated by designing a thermodynamic cycle and integrating along the relevant paths. Such paths can either be real chemical processes or alchemical processes. A good example of the alchemical process is the Kirkwood's coupling parameter method.[1]
Free energy can be expressed by
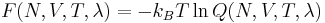 ,
,
where λ=0 represents state A and λ=1 state B. If we take the derivative of F with respect to λ, we will get that it equals the ensemble average of the derivative of potential energy with respect to λ.
Thus the free energy difference of different states can be computed from the difference of potential energy. Umbrella sampling is a related free energy method. It adds a bias to the potential energy. In the limit of an infinite strong bias it is equivalent to thermodynamic integration.[2]
See also
References
- ^ J. G. Kirkwood. Statistical mechanics of fluid mixtures, J. Chem. Phys., 3:300-313,1935
- ^ J Kästner et al. (2006). "QM/MM Free-Energy Perturbation Compared to Thermodynamic Integration and Umbrella Sampling: Application to an Enzymatic Reaction". JCTC 2 (2): 452–461. doi:10.1021/ct050252w.